問題 サイコロが3つある。3個同時にふる場合の目の組み合わせを列挙せよ。
今回はまずこの問題を考える。前回と違うのは1,1,1という目の重複が許される点だ。
for(int i=1;i<=6;i++) {
for(int j=i;j<=6;j++) {
for(int k=j;k<=6;k++) {
System.out.println("["+i+j+k+"]");
}
}
}3つの目を作るので3重ループを回すところまでは前回と同じだが、重複を許すので基本はすべての目の組み合わせを考える。この際、内側のループの開始を外のループと一致させることで[1,1,2]に対する[1,2,1]などの同じ組み合わせの登場を防ぐことができる。(i<=j<=kの関係となっている)
実行例
[111] [112] [113] [114] [115] [116] [122] [123] [124] [125] [126] [133] [134] [135] [136] [144] [145] [146] [155] [156] [166] [222] [223] [224] [225] [226] [233] [234] [235] [236] [244] [245] [246] [255] [256] [266] [333] [334] [335] [336] [344] [345] [346] [355] [356] [366] [444] [445] [446] [455] [456] [466] [555] [556] [566] [666]
確認問題
Q1
以下のお菓子の中から2つを選択する(重複可)。ただし、合計金額は200円以内でなければならない。 アメ:30円 チョコ:120円 ガム:100円 ポテチ:80円 ビスケット:90円 条件を満たす組み合わせをすべて列挙せよ。 出力フォーマットは以下のようにすること [アメ(30),アメ(30)] [アメ(30),チョコ(120)] . . .
public class Main {
public static void main(String[] args) {
Snack[] snacks={
new Snack("アメ",30),
new Snack("チョコ",120),
new Snack("ガム",100),
new Snack("ポテチ",80),
new Snack("ビスケット",90),
};
for(int i=0;i<snacks.length;i++){
for(int j=i;j<snacks.length;j++){
if(snacks[i].price+snacks[j].price<=200){
System.out.printf("[%s,%s]%n",snacks[i],snacks[j]);
}
}
}
}
}
class Snack{
String name;
int price;
Snack(String name,int price){
this.name=name;
this.price=price;
}
@Override
public String toString() {
return String.format("%s(%d)", this.name,this.price);
}
}選ぶ個数が増えてきたら・・・
問題
赤、緑、青のボールがたくさんある。5個選ぶ場合の組み合わせを列挙せよ。
ではこの問題はどうだろうか?確かにこの問題も5重forを使って先ほどと同じように解くことができる。
public class Main {
public static void main(String[] args) {
String[] colors= {"R","G","B"};
for(int i=0;i<3;i++) {
for(int j=i;j<3;j++) {
for(int k=j;k<3;k++) {
for(int l=k;l<3;l++) {
for(int m=l;m<3;m++) {
System.out.printf("[%s,%s,%s,%s,%s]%n",
colors[i],
colors[j],
colors[k],
colors[l],
colors[m]
);
}
}
}
}
}
}
}[R,R,R,R,R] [R,R,R,R,G] [R,R,R,R,B] [R,R,R,G,G] [R,R,R,G,B] [R,R,R,B,B] [R,R,G,G,G] [R,R,G,G,B] [R,R,G,B,B] [R,R,B,B,B] [R,G,G,G,G] [R,G,G,G,B] [R,G,G,B,B] [R,G,B,B,B] [R,B,B,B,B] [G,G,G,G,G] [G,G,G,G,B] [G,G,G,B,B] [G,G,B,B,B] [G,B,B,B,B] [B,B,B,B,B]
ただもし、10個選ぶとなったら10重forだろうか?この方法では限界がありそうだ。
//何かしら五個選ぶ...どうしよう
○○○○○
//2つ線を引いて3つの部屋に分けるという「神」発想
○|○○|○○ ->この場合赤が1,緑が2,青が2と考える
||○○○○○ ->これは赤0,緑0,青5
|○○○|○○ ->これは赤0,緑3,青2
○○○○○|| ->これは赤5,緑0,青0縦棒を引いて3つの部屋に分けるという発想が素晴らしい。これでこの問題は7個ある場所から2つの縦棒の位置を決めるという。単なる組み合わせ問題になってしまった。(7C2) 。2つの縦棒を決めるだけなら選ぶ個数が10個でも100個でも2重for文で解決できる。
単なる組み合わせ問題の解き方がわからない人はまずはこちらから学習してもらいたい。
7つの場所を0~6で表してその中のどこの部分が縦棒なのかを考えていく。
0 1 2 3 4 5 6
| |Javaで求めてみよう。
public class Main {
public static void main(String[] args) {
int n=5;//個数
for(int i=0;i<n+1;i++){
for(int j=i+1;j<n+2;j++){
System.out.printf("%d,%d%n",i,j);
}
}
}
}[結果]
0,1 0,2 0,3 0,4 0,5 0,6 1,2 1,3 1,4 1,5 1,6 2,3 2,4 2,5 2,6 3,4 3,5 3,6 4,5 4,6 5,6
縦棒の組み合わせは上記の21個あることがわかった。
実際にプログラムで縦棒を入れながら赤(R)緑(G)青(B)で表示してみよう。
public class Main {
public static void main(String[] args) {
int n=5;
for(int i=0;i<n+1;i++){
for(int j=i+1;j<n+2;j++){
//System.out.printf("%d,%d%n",i,j);
//7回回す
for(int k=0;k<n+2;k++){
if(k<i){
//kの値がiより小さい場合はRを出力
System.out.print("R");
}else if(k==i || k== j){
//kの値がiとjと等しい場合は縦を出力
System.out.print("|");
}else if(k>j){
//kの値がjより大きい場合はBを出力
System.out.print("B");
}else{
//それ以外はG
System.out.print("G");
}
}
System.out.println();
}
}
}
}[結果]
||BBBBB |G|BBBB |GG|BBB |GGG|BB |GGGG|B |GGGGG| R||BBBB R|G|BBB R|GG|BB R|GGG|B R|GGGG| RR||BBB RR|G|BB RR|GG|B RR|GGG| RRR||BB RRR|G|B RRR|GG| RRRR||B RRRR|G| RRRRR||
縦棒の位置を決めることによってすべての組み合わせが求められたようだ。
以下のようなフォーマットでの出力を考えよう。
R G B [0,0,5] [0,1,4] [0,2,3] [0,3,2] [0,4,1] [0,5,0] [1,0,4] [1,1,3] [1,2,2] [1,3,1] [1,4,0] [2,0,3] [2,1,2] [2,2,1] [2,3,0] [3,0,2] [3,1,1] [3,2,0] [4,0,1] [4,1,0] [5,0,0]
個数をカウントしていこう。まずRの個数だが下の図を見てもわかるがこれはiの値だ
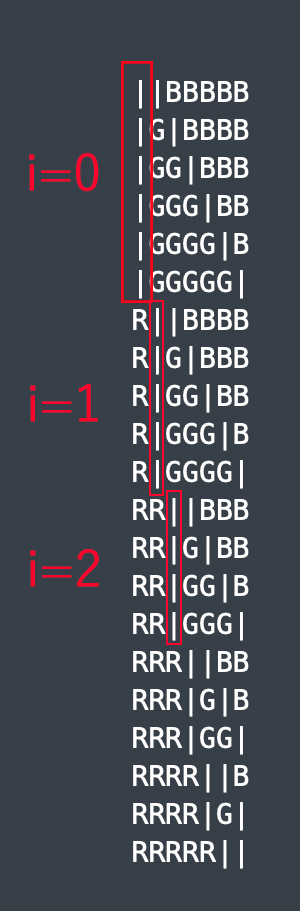
ソースコードに落とし込もう。
public class Main {
public static void main(String[] args) {
int n=5;
System.out.println(" R G B ");//追記
for(int i=0;i<n+1;i++){
int rCount=i;//iの値は赤の数
for(int j=i+1;j<n+2;j++){
int gCount=j-rCount-1;//緑の数はj-赤-1
int bCount=n-rCount-gCount;//青はn-赤-緑
System.out.printf("[%d,%d,%d]",rCount,gCount,bCount);
System.out.println();
}
}
}
}最初の問題の答えを求めることができた。重複組合せ問題はパターンにもよるが今回のように補助の縦棒を加えて単なる組み合わせ問題にしてしまうと解決することがある。
取りうる値の可能性から考える
こういった時は取りうる値の可能性からのループを組む方法がある。
for(int i=5;i>=0;i--) {
for(int j=5-i;j>=0;j--) {
System.out.printf("[%d,%d,%d]%n",i,j,5-i-j);
}
}まず、赤の個数の可能性を考え(5~0)次に内側のループでは緑の個数の可能性について考える。その際に赤のボールに使った個数は初期値設定の際に減らすのがポイントだ。2つの数がわかれば残りが青ということになる。
確認問題
500円、100円、50円、10円を組み合わせは自由に10枚使ってできる金額の種類と総数を求める処理を作成せよ
100 140 180 . . . 4550 4600 5000 244種類
public class Main {
public static void main(String[] args) {
Set<Integer> moneys=new TreeSet<>();
for(int i=10;i>=0;i--) {
for(int j=10-i;j>=0;j--) {
for(int k=10-i-j;k>=0;k--) {
//System.out.printf("[%d,%d,%d,%d]%n", i,j,k,10-i-j-k);
moneys.add(i*500+j*100+k*50+(10-i-j-k)*10);
}
}
}
for(int m:moneys) {
System.out.println(m);
}
System.out.println(moneys.size()+"種類");
}
}応用
先程のお菓子の問題は2つを選んだがこれを予算以内ならばいくつでもOKという問題にしてみよう。
以下のお菓子の中から自由に選択する(重複可)。ただし、合計金額は200円以内でなければならない。 アメ:30円 チョコ:120円 ガム:100円 ポテチ:80円 ビスケット:90円 条件を満たす組み合わせをすべて列挙せよ。 出力フォーマットは以下のようにすること(出力順は任意) [ビスケット(90),] [ビスケット(90),ビスケット(90),] [ポテチ(80),] [ポテチ(80),ビスケット(90),] [ポテチ(80),ポテチ(80),] [ガム(100),] . . .
解法1
この程度ならfor文ですべての組み合わせをとってもどうにかなる。
public class Main {
public static void main(String[] args) {
Snack[] snacks = {
new Snack("アメ", 30),
new Snack("チョコ", 120),
new Snack("ガム", 100),
new Snack("ポテチ", 80),
new Snack("ビスケット", 90),
};
int maxMoney=200;//この金額を超えてはいけない
//アメは0~6個の可能性
for(int i=0;i<=maxMoney/snacks[0].price;i++){
//チョコは0~1個の可能性
for(int j=0;j<=maxMoney/snacks[1].price;j++){
for(int k=0;k<=maxMoney/snacks[2].price;k++){
for(int l=0;l<=maxMoney/snacks[3].price;l++){
for(int m=0;m<=maxMoney/snacks[4].price;m++){
boolean isCountOK=i+j+k+l+m >=1;
boolean isPriceOK=i*snacks[0].price+j*snacks[1].price+k*snacks[2].price+l*snacks[3].price+m*snacks[4].price <=maxMoney;
if(isCountOK && isPriceOK){
System.out.printf("[%s%s%s%s%s]%n",
snacks[0].showInfoTimes(i),
snacks[1].showInfoTimes(j),
snacks[2].showInfoTimes(k),
snacks[3].showInfoTimes(l),
snacks[4].showInfoTimes(m));
}
}
}
}
}
}
}
}
class Snack {
String name;
int price;
Snack(String name, int price) {
this.name = name;
this.price = price;
}
@Override
public String toString(){
return String.format("%s(%d)", this.name,this.price);
}
String showInfoTimes(int times){
String ret="";
for(int i=0;i<times;i++){
ret+=toString()+",";
}
return ret;
}
}
実現はできたが力技感がすごい、しかもお菓子が増えたときの修正が面倒だ。
こういったときには再帰処理を検討してみるとよい。
解法2(再帰)
import java.util.*;
public class Main {
static final List<Map<Snack,Integer>> data=new ArrayList<>();
public static void main(String[] args) {
List<Snack> snacks=new ArrayList<>();
snacks.add(new Snack("アメ", 30));
snacks.add(new Snack("チョコ", 120));
snacks.add(new Snack("ガム", 100));
snacks.add(new Snack("ポテチ", 80));
snacks.add(new Snack("ビスケット", 90));
Map<Snack,Integer> map=new LinkedHashMap<>();
getSnack(200,snacks,map);
}
static void getSnack(int money, List<Snack> snacks, Map<Snack,Integer> map) {
//探索するお菓子がなくなったら終わり
if(snacks.size()==0){
//結果出力
for(Snack key:map.keySet()) {
for(int i=0;i<map.get(key);i++) {
System.out.print(key+",");
}
}
System.out.println();
}else {
//着目するお菓子(リストの先頭から取り出す(リストは短くなる))
Snack snack = snacks.remove(0);
//アメだったら0~6個の可能性がある
for (int i = 0; i <= money / snack.price; i++) {
if(i !=0) {
map.put(snack, i);
}
//アメの個数ごとに再帰処理(残金,一つ短くなったリスト,更新されたMap)
getSnack(money - snack.price * i, new ArrayList<Snack>(snacks), new LinkedHashMap<Snack,Integer>(map));
}
}
}
}
class Snack {
String name;
int price;
Snack(String name, int price) {
this.name = name;
this.price = price;
}
@Override
public String toString() {
return String.format("%s(%d)", this.name,this.price);
}
}
import java.util.ArrayList;
import java.util.List;
public class Main {
public static void main(String[] args) {
List<Snack> snacks=new ArrayList<>();
snacks.add(new Snack("アメ", 30));
snacks.add(new Snack("チョコ", 120));
snacks.add(new Snack("ガム", 100));
snacks.add(new Snack("ポテチ", 80));
snacks.add(new Snack("ビスケット", 90));
getSnack(200,snacks,0,"");
}
static void getSnack(int money, List<Snack> snacks, int count,String result) {
//探索するお菓子がなくなったら終わり
if(snacks.size()==0){
//個数2個以上が今回の出力対象
if(count>=2){
System.out.println("["+result+"]");
}
}else {
//着目するお菓子(リストの先頭から取り出す(リストは短くなる))
Snack snack = snacks.remove(0);
//アメだったら0~6個の可能性がある
for (int i = 0; i <= money / snack.price; i++) {
//アメの個数ごとに再帰処理(残金,一つ短くなったリスト,買った個数増やす,今買った要素を文字にして連結)
getSnack(money - snack.price * i, new ArrayList<Snack>(snacks), count + i,result+snack.showInfoTimes(i));
}
}
}
}
class Snack {
String name;
int price;
Snack(String name, int price) {
this.name = name;
this.price = price;
}
String showInfo(){
return String.format("%s(%d)", this.name,this.price);
}
String showInfoTimes(int times){
String ret="";
for(int i=0;i<times;i++){
ret+=showInfo()+",";
}
return ret;
}
}
再帰はロマンだ。ソースを見たときに処理が分かりづらいという弱点はあるが時として超絶なパワーを発揮する。プログラミング上級者を目指すならば必ずマスターしていかなければならない項目だ。
おまけ
1セント,10セント,25セントのコインを好きな枚数使う事ができる. 1234セントを支払う時最低何枚で払うことが出来るか?再帰を用いて求めよ。
import java.util. *;
public class Main {
static int min=1000000; //答えとなる最小枚数(初期値として適当に大きな数字をいれておく)
public static void main(String[] args){
List<Integer> list=new ArrayList<>();
list.add(25);
list.add(10);
list.add(1);
change(1234,list,0,"");
System.out.println("最小は"+min+"枚");
}
static void change(int money,List<Integer> list,int num,String result){
if(list.size()==0){
if(money==0){
if(num<min){
min=num;
}
System.out.printf("%d枚%s%n", num,result);
}
}else{
int coin=list.remove(0);
for(int i=0;i<=money/coin;i++){
change(money-coin*i,new ArrayList<Integer>(list),num+i,result+coin+"("+i+")");
}
}
}
}



コメント